2020. 6. 4. 15:58ㆍ자료구조\알고리즘
1. 가장 단순한 문자열 검색
가장 단순한 문자열 검색은 문자열의 시작부터 마지막까지 하나씩 주어진 패턴이 존재하는지 확인하는 방법입니다. 예를 들어 텍스트 “ABCABABCDE”에서 패턴 “ABC”가 어디서 등장하는지 찾아봅니다. 패턴 “ABC”를 시작부터 한 자리씩 옮기면서 같은지 비교합니다.








위의 그림과 같은 과정을 보면 “ABCABABCDE”에서 패턴 “ABC”는 두 번 등장함을 알 수 있습니다. (녹색 네모로 표시된 그림이 일치하는 경우) 이 과정의 시간 복잡도는 텍스트의 길이를 N, 패턴의 길이를 M이라 할 때, 각 텍스트의 인덱스에 대해 패턴이 일치하는지 비교하므로 O(NM)입니다.
2. KMP 알고리즘이란
KMP 알고리즘을 이해하기 위한 사전 지식
우선 KMP 알고리즘을 이해하기 위해 먼저 알아야 하는 2가지가 있습니다. 첫 번째는 접두사(prefix)와 접미사(suffix)입니다. 예를 들어 “banana”의 접미사와 접두사를 보겠습니다.
<banana의 접두사>
b
ba
ban
bana
banan
banana
<banana의 접미사>
a
na
ana
nana
anana
banana
두 번째는 pi배열입니다.pi[i]는 주어진 문자열의 0 ~ i 까지의 부분 문자열 중에서 prefix == suffix가 될 수 있는 부분 문자열 중에서 가장 긴 것의 길이를 말합니다. 예를 들어 “ABAABAB”의 pi배열을 구해봅니다.
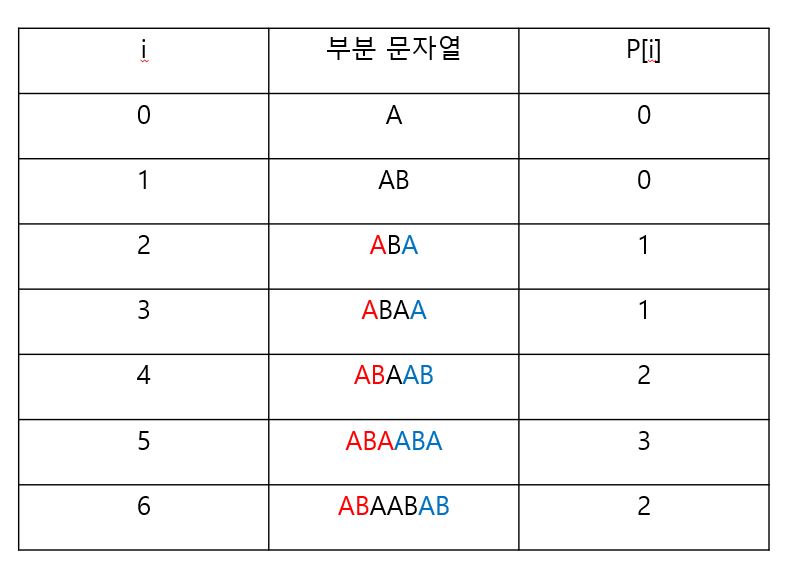
위 그림과 같이 접미사와 접두사가 일치하는 문자열의 가장 긴 길이를 포함하는 배열이 pi 배열입니다.
KMP 알고리즘이란?
KMP 알고리즘은 접두사와 접미사의 개념을 활용하여 ‘반복되는 연산을 얼마나 줄일 수 있는지’를 판별하여 매칭할 분자열을 빠르게 점프하는 기법입니다. 예를 들어 “ABCDABCDABEE”에서 패턴 “ABCDABE”를 찾는 상황을 생각해봅니다.


첫 번째 시도를 보면 빨간 부분이 틀렸다는 사실 만이 아니라 녹색 부분은 일치한다는 사실을 알 수 있습니다.

이처럼 틀린 부분 앞 문자열을 확인하면 “AB”라는 문자열이 접두사와 접미사로 있는 것을 확인할 수 있습니다. 그 결과로 마지막 문자열의 P[5]의 값은 2라는 정보를 이용해 우리는 다음 탐색을 아래와 같이 진행할 수 있습니다.

이처럼 KMP 알고리즘은 틀렸다는 사실이 아니라 조금이라도 일치했었다는 정보에 주목하기 미리 전처리 해둔 pi배열을 이용해 많은 중간 시도를 건너뛸 수 있게 합니다.
KMP의 구현
P[i] 배열 구하기
public int[] getPi(String s) {
int length = s.length();
int j = 0;
int pi[] = new int[length];
for(int i = 1; i < length; i++) {
while(j > 0 && s.charAt(i) != s.charAt(j)) {
j = pi[j - 1];
}
if(s.charAt(i) == s.charAt(j)) {
pi[i] = ++j;
}
}
return pi;
}KMP 알고리즘
public List<Integer> kmp(String s, String pattern) {
List<Integer> list = new ArrayList<>();
int pi[] = getPi(pattern);
int n = s.length();
int m = pattern.length();
int j = 0;
for(int i = 0; i < n; i++) {
while(j > 0 && s.charAt(i) != pattern.charAt(j)) {
j = pi[j - 1];
}
if(s.charAt(i) == pattern.charAt(j)) {
if(pattern.charAt(j) == m - 1) {
list.add(i - m + 1);
j = pi[j];
} else {
j++;
}
}
}
return list;
}참조: https://bowbowbow.tistory.com/6
'자료구조\알고리즘' 카테고리의 다른 글
| 카데인 알고리즘 (0) | 2021.10.19 |
|---|---|
| Huffman Coding (0) | 2020.11.27 |
| Tim sort (0) | 2020.09.11 |
| 아호 코라식 알고리즘 (0) | 2020.06.04 |
| 트라이 (0) | 2020.06.04 |